Strengthening of the Italian Research Infrastructure for Metrology and Open Access Data in support to the Agrifood
INRIM2 – Advanced materials metrology and life sciences
(Reference person: Alessandra Manzin)
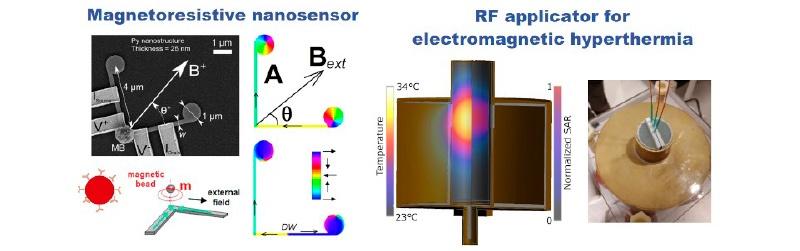
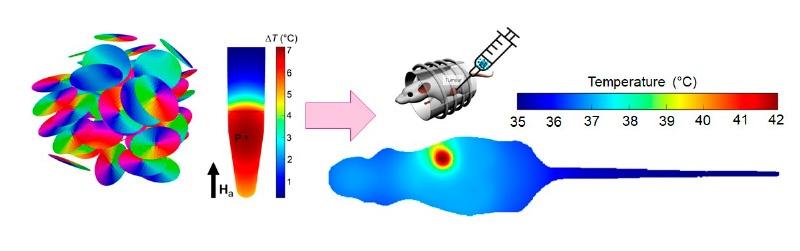
The OU has an internationally recognised experience in the development of mathematical models and numerical tools for the simulation of physical phenomena in materials, devices, sensors and biological systems. This is achieved by integrating competences in numerical modelling, High-Performance Computing (HPC) and data analysis. Specific attention is devoted to the engineering and optimisation of the numerical tools to virtually reproduce as realistic as possible the physical phenomena investigated, with a high computational efficiency. To this aim, parallel computing based on Graphics Processing Units is exploited together with the implementation of advanced numerical methods. The OU operates in the framework of an already active computing infrastructure, equipped with a HPC cluster based on a hybrid CPU-GPU architecture, and workstations for software development, post-processing, data analysis and large-scale data storage. The expertise of the OU has been addressed to research activities that comprise the multiscale modelling of materials (down to the nanoscale) and the interactions of nanomaterials with biological systems. Within EURAMET, the OU is a member of the European Metrology Network for Mathematics and Statistics (Mathmet), which supports the application of mathematical and statistical tools in measurement science across Europe, and promotes the development of new research fields, like Artificial Intelligence.
Numerical modeling of miniaturized sensors and devices
Design of nanomaterials for therapeutic applications
Numerical reconstruction of MRI images of digital phantoms
Alessandra Manzin
Is Senior Researcher at INRiM, where leads the Scientific Unit “Biomedical Sciences and Technologies”. Her main expertise covers the fields of numerical modeling and high-performance computing, with a focus on computational electromagnetism, nanotechnology and material science. She has been involved with WP leading roles and/or as INRiM reference contact in several EURAMET projects as well as in Horizon H2020 and national projects, and is a member of the European Metrology Network for Mathematics and Statistics (Mathmet). She has authored over 110 papers in international journals (h-index 23, Google Scholar) and served as an Editor for IEEE-sponsored conferences and international journals. Her research interests include the development of advanced numerical models for life science, nanotechnology and metrology applications, e.g., design of nanomaterials, miniaturized sensors and devices for diagnostics and therapeutics, combined with in silico modeling.
Riccardo Ferrero
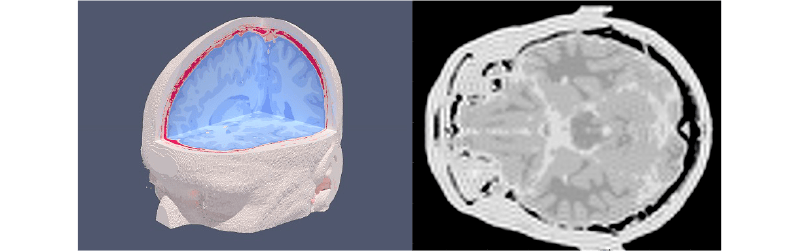
Received the M.Sc. degree in Mathematical Engineering and the Ph.D. degree in Metrology cum laude from the Politecnico di Torino in 2014 and 2019, respectively. He is currently a researcher within the Scientific Unit “Biomedical Sciences and Technologies”. His research field is the development of numerical codes for the study of devices, systems and materials for therapeutic and diagnostic applications. He actively contributes to the development of numerical solvers for the Landau-Lifshitz-Gilbert equation to investigate the properties of magnetic nanomaterials, as well as numerical models to simulate nanomaterial release and behavior in tissues. He developed a numerical solver for the Bloch equation to reconstruct MRI imaging processes, to build digital phantoms, and to perform sensitivity analysis of qMRI.
Marta Vicentini
Received the M. Sc. Degree in Mathematics cum laude from the University of Torino in 2018 and the Ph.D degree in Metrology cum laude from the Politecnico di Torino in 2022. She is currently a Junior Researcher in the Scientific Unit “Biomedical Sciences and Technologies”. Her research field is the development of mathematical models and numerical codes for the study of devices and materials for biomedical applications, for both therapeutic and diagnostic purposes. She is focused on the implementation of in silico models and data analysis tools for the simulation and the study of physical phenomena in biological systems, with specific attention to the optimization of the numerical methods to guarantee the reliability of the numerical solutions, as well as the high computational efficiency of the models.